明日は旧暦の７月７日にあたる。
　七夕が雨だったり満月だったりするたびに、七夕だけは旧暦(太陰太陽暦)に戻すべきだと思うんだけど、調べてみると国立天文台も似たような主張をしていた。

　太陰太陽暦は、明治6年に現在の暦が採用されるよりも前の暦で、現在は公には使われていません。このため、伝統的七夕の日は、太陰太陽暦による7月7日に近い日として、以下のように定義します。
　二十四節気の処暑（しょしょ＝太陽黄経が150度になる瞬間）を含む日かそれよりも前で、処暑に最も近い朔（さく＝新月）の瞬間を含む日から数えて7日目が「伝統的七夕」の日です。

国立天文台webサイトより

　やけにまわりくどいのは、政府が採用していない旧暦を国立機関が奨励するわけにはいかない、という事情と、より厳密に星空が見やすい日を、という計算による。
　これによると今年の七夕は８月６日だが、来年は８月２４日までずれこむ。
　ちょっと年中行事にするには苦しいかもしれない。

　だが、よく考えたら明治政府が太陽暦を採用したときにその旨を織姫と彦星に報告したとは考えにくいので、彼らはまだ普通に旧暦７月７日に会ってるのかもしれない。
　いまさら国立天文台が「伝統的七夕」を通達したところで、それが織女星に届くまで光速でも２５年かかるので、いっそみんな旧暦で七夕をすべきじゃあないだろうか？

[LINK] [COMMENT]

　長さの単位は「メートル」、時間の単位は「秒」。
　そして速度は「秒速○○メートル」とか「○○メートル毎秒」と表される。

　……なぜ速度の単位には名前がないんだろう？
　１秒ごとに10メートル進むから「10メートル毎秒」。わかりやすい。
　だが、スマートじゃあないと思う。

　「1秒間に1ジュールぶんの仕事をする仕事量」を1ワットとしたではないか。
　「1時間に1海里進む速度」には1ノットという名前があるではないか。
　なぜ「1秒間に1メートル進む速度」に名前をつけなかった！？
　ワットとかより頻繁に使うくせに「時速40キロメートル」とか煩雑だろ！
　加速度の単位が「1メートル毎秒毎秒」になったときに、誰もツッコまなかったのか！


　我々が古くから使っている単位は、身近なものをモノサシにしたものが多い。
　フィートとかエーカーとかの単位が消滅しないのは、イメージしやすいからだ。
　日本人だってまだ「四畳半」くらいの感覚はあるだろう。
　ひと世代後にはどーなってるかわからないけど。

　不動産表示に使われる「徒歩1分」は、80メートルのことらしい。
　分速80メートルを「徒歩の速度」として定義しているわけだ。
　「速度」という概念を編み出した人が、真っ先にこれを使うべきだったのではないか。

　いや待て、速度という概念を編み出した人って何だ？
　ワットやパスカルと違って、そういう人がいないんじゃないのか。
　こうなると、誰か有名な人にご登場頂かなければならない。

　現在人類最速の男、ウサイン・ボルトは、平均時速37キロメートル強で走るらしい。
　この速さを単位にすれば、「ボルトの2倍速えー！」という感じでイメージしやすい。
　37km/hを「1ボルト」として定義して……ピカチュウ速えー！


　昔の人が、速度の単位に名前をつけなかったのは、
　誰もがイメージできる速度のモノがなかった、というのももちろんだが、
　そもそも速度を定量的に示す必要があまりなかった、という可能性もある。
　人間同士とか馬同士だったらもう競走しちゃうだろうし、矢は比較するには速すぎる。
　「サラマンダーより、ずっとはやい！！」で足りていたのだ。

　よく考えたら我々だってそうだ。
　ネズミ捕りのポリスメンがいなかったら、時速なんて生活の中に登場しない。
　速度……身近だと思っていたが、意外となじみが浅い単位だったんだな……。

[LINK] [COMMENT]

　人類はふだん10進法でモノを数えていて、たいして意識しないけど、世の中、10進法以外を採用しているものはけっこう多い。

　たとえば(これは厳密にはｎ進法とは違うけど)なぜ時間(hour)は12進法なのか。
　12は割りやすいから、というのが真っ先に思いついたが、半分→半分→半分というふうに8分割できないのは大きな弱点ではないか？
　割りやすさが理由なら、もっと割りやすい数にできるだろう。いったいなぜ？



　調べてみると、めそ…ゲフンゲフン！
　めそぽタミヤ文明までさかのぼった。
　さすが静岡が誇る世界のタミヤ。

　めそぽタミヤの人は、月が12回まるくなるとだいたい季節が一巡することを知って、暦を作った。
　そのときどうやら「12ってのは何かスゴイらしい」と悟ったようだ。
　それで、昼間を12分割して時刻を表すことにして、夜は夜でまた12分割した。
　これがAM/PMの始まり、らしい。

　この場合の昼・夜は「日の出～日没」を基準に考えられていたので、最初は「1時間」の示す長さが季節によって違っていた。
　これを昼夜ぶっ通しにひきのばして、24時間を平均的にならしたのが、ギリシャの天文学者・ひっぱるコスという人のようだ。

　月がだいたい30日でまるくなって、それが12回で季節が一巡するとなると、一年がだいたい360日。角度が360進法なのは偶然の一致ではあるまい。
　英語でも11と12はガッツで単語を作っている。
　elevenの語源は「10と残り(lve)１つ(e)」、twelveの語源は「残り(lve)２つ(twe)」らしいので、英語圏の人も「俺、指10本しかないけど、それはそれとして12スゲー」と思っていたのだろう。

　こうしてみると、10進法のほうがむしろ不自然な行いのような気がする。
　我々が10本指でなかったら、誰がこんな不便な底を使うか！



　つまり、何気ないことに思えるかもしれないが、
　「ひぐらし」の世界はおそらく８進法で回っていて、
　あの世界には８・９という数字はないのだ。
　呪いよりなにより、俺はそのほうが「異世界」を感じる。

[LINK] [COMMENT]

　よく「スズメの涙ほど」って言うけど、実際どの程度なんだ？
　そう思った俺はすぐに電卓とブラウザを立ち上げた。

　まずスズメの全長と体重を調べる。
　成鳥で15センチ、25グラムってとこらしい。

　次に横から撮ったスズメの写真を使って、全長と目の大きさの比率を測る。
　全長を15センチとすると、目の直径はおよそ0.4センチ。4ミリだ。

　目は球体だが、露出してる部分をだいたい円形の平面と見なすと、その面積はおよそ12.6平方ミリ。両目あわせて25平方ミリでよかろう。
　これでスズメの目の大きさが概算できた。

　さて次に涙の量だが、スズメは涙を流さない。
　ロボットじゃないけど。マシーンじゃないけど。ダダッダー。
　だけどわかるぜ、涙の厚み。

　人間の目に張られている涙の厚さを調べると、7マイクロメートル程度とのこと。
　7マイクロ！0.007ミリの驚きの薄さ！
　これがスズメの目にもあると仮定すると、さきほどの目の面積から、涙の体積はおよそ0.175立方ミリ。
　これがスズメ１羽の目に常時存在するおおよその涙の量。

　この体積から涙の重さを計算する。涙は90％以上が水だ。
　1立方ミリメートルの水の質量をおおよそ1ミリグラムとすると、スズメの涙の重さは、概算に概算を重ねて、0.175ミリグラムだ！
　砂粒１個がおよそ1ミリグラムなので相当な少なさと言える。

　スズメ本体を25グラムとすると、本体：涙＝143000:1 の重量比となる。
　本体に対しておよそ0.0007％だ。
　凄まじい小ささだぞスズメの涙！定期預金の利息なんてこの100倍近くあるぞ！



　しかし文系脳で考えると、この場合の涙は「雫となってこぼれた涙」を指すのではないかと解釈できる。
　スズメは涙を流さないので、これは測定できない。
　誰か、スズメとスズメの涙の界面張力を知ってる人、計算してくれ。

[LINK] [COMMENT]

　僕自身はめったに買わないが、年末になると宝くじ売り場が盛況だ。

　宝くじの賞金の期待値は、価格のおよそ半分。
　300円で買った宝くじは、1枚あたり150円弱の賞金が期待できる。
　これは法律で「半分を超えちゃ駄目」と決められているから。

　だが、この期待値を見て「買う人は愚かだ」と結論づけるのは早計だ。
　期待値を利用するときは、かならず分散をチェックしなければならない。
　宝くじの賞金は0から3億まであるから、分散はかなり大きい。
　期待値と違って具体的な数字にならないため忘れられがちだが、「結果がどの程度バラつくか」は我々の行動に大きな影響を与えている。

　みんな期待値が150円弱であることを承知して「宝くじは夢を買うものだ」と言う。
　夢という曖昧なワードを排除すると、これは分散を買っているということだ。
　嫌な分散を小さくするために、保険会社に金を払う人がたくさんいる。
　良い分散を大きくするために、150円を払ってもよかろう。

　僕はこの分散を評価していないわけではない。
　今年に限っては、期待値・分散以外の「買わない理由」があるのだ。
　ここまでしてきた論理的な話では全くない。

　今年、プロゴルファーの小田龍一選手が、賞品として宝くじ3000枚を獲得した。
　これは要するに、3枚だけ買った人に比べて、小田選手は1000倍も当たりやすい、という事だ。
　気合を入れて30枚買ったとしても、まだその100倍も当たりやすい人がいるという事実。
　この圧倒的な開き。どう考えても太刀打ちできそうにない。
　バッファローマンに「わたしの超人強度は1000万パワーだ！」と言われたウォーズマンの気分だ。
　もはや白旗、完全降伏である。


　同じ確率的アプローチでもこれほど印象に差が出ることがある、と身をもって知った。

[LINK] [COMMENT]

　唐突に「定規とコンパスだけで正五角形を作図せよ」という問題が出された。

　ちょっと考えたがサッパリわからない。
　敵を知らずして闘いに臨むべきではなかろう。
　まずは正五角形の特徴を調べることにした。
　いきなり正五角形の作図法を調べても、理解も証明も困難だろう、という判断だ。

　まず、正多角形なので、全ての辺の長さが一緒だ。
　内角は108度。煩悩の角度である。３つの三角形に分断して証明した覚えがある。

　特筆すべきは、辺の長さと、対角線の長さの比率が「黄金比」になっている点だ。
　ややめんどくさいが、三角形の合同＆相似と解の公式を使えば証明できる。
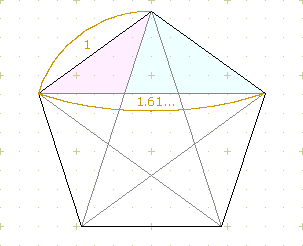　黄金比。聞いたことがあるか？
　およそ1:1.618。これは古代から最も美しい形の基本の比率とされている。
　『パルテノン神殿』『ミロのビーナス』……この世の建築・美術の傑作群には、偶然なのか？あるいは計算なのか？この黄金比が隠されている。
　自然界にもたびたび現れる比率だ、とロバート・ラングドン先生も言っていた。
　ちなみに正方形の一辺と対角線の比(1:1.41…)は「白銀比」と呼ばれ、コピー用紙とかに使われている。
　なるほど、正四角形が白銀比で、正五角形が黄金比ってわけか。

　とにかくその黄金比が得られれば、五角形の辺の長さから対角線の長さが分かるわけで、コンパスで残りの点をガチャガチャ探り当てて、この問題はゲームセットだ。

　黄金比、黄金比……

　まて……芸術家たちはどこから「黄金比」を学んだ？
　「美しさの基本」とかを、どこで？
　学者から聞いたり、定規で計ったわけじゃあないはずだ……
　それはコピーってやつで、本物じゃあない……本物があるはずだ！

　ぼくが……今！この目で見ているものでいいのか！？
　今までにも！すでに！さっきからも！見ているもので！！
　LESSON4……敬意を払え！
　俺の肉体で五角形を作図するッ！
　どこかがきっと黄金比なハズだァー！！


　真面目な解答は、真面目な黄金比の作図法を調べていただければ、中学校の数学ツールだけでも辿り着けると思うので、割愛。

[LINK] [COMMENT]

　よく「数学は社会とかと違って、答えがきっちり１つに決まる」みたいな比較がある。
　これはある意味では正しいが、かならずしもそうとは言えない。

　小学校の段階で、すでに数学は不安定である。
　３年生の教科書で「割り算」が登場するが、当然その中には「ゼロ除算」が含まれる。
　しかし、手元の教科書には「ゼロで割ってはいけない」という内容の説明が無い。

　いったい教室ではどうやって切り抜けているのだろう。
　「０÷４＝０」が示されているのに、「４÷０」について疑問を持つ子どもが一人もいない、なんてことがあるだろうか。

　数学の世界が崩壊してしまうようなバグが、小学校３年生の段階で露呈してしまう。
　これを不安定と言わずして何と言うのか。


　しかし、虚数なんかもかまわないで定義してきた数学である。
　「ゼロをゼロで割った数」みたいなものを定義した人はいなかったのだろうか。
　なんかこう、それっぽい記号をあてがって「ゼロで割るとコレが出てきちゃってすごい高度な数学になるヨ！」みたいなハッタリを効かせれば、小学生もとりあえず矛を収めてくれるのではないか。

　それっぽい記号か…
　ゼロをゼロで割ったことを示すために「％」みたいな形でどうか？
　あれ、なんですでにキーボードに刻印されてんだ、この記号。

[LINK] [COMMENT]

　正方形は台形である。

　小学校の算数で習ってから随分たつが、やはり引っかかる。
　論理的には間違っていない。
　台形は「少なくとも一組の対辺が互いに平行な四角形」なので、正方形は台形だ。
　……が、なんか引っかかる。
　「正方形は四角形である」と言ったときの自然さと比べて、この不自然さは何だ？

　ある日、この疑問を一発で解決してくれるアスキーアートがあることに気づいた。
　「いいの！？それ、タンヤオでいいの！？」
　……というこのMOTTAINAI感覚が、ピッタリこの感覚にあてはまる。

　正方形は、そうとう甘く判定しても、自然界にはまず現れない。
　台形であるだけでなく平行四辺形でもあり、ひし形かつ長方形である「正方形」を台形と称するのは、そのレアさから考えると「大四喜字一色四暗刻をトイトイ扱い」くらいのMOTTAINAI出来事といっていいだろう。

　「正方形は四角形である」と言ったときに不自然さを感じないのは「四暗刻は麻雀の役である」と似た捉えかたをするからだろうか。
　そんなことまで考えていたら「正方形」が麻雀の役に見えてきた。
　「ジュンチャン・サンシキ・セーホーケー・ドラドラ」みたいにスルッと紛れ込んでくる。

[LINK] [COMMENT]

　インクジェット対応のCD-Rに何かを印刷するとき、印刷できる部分の直径がわからなくって、穴の周辺に定規をあてて一番長い所を探す……なんてことが日常生活では頻繁にあるよね！
　そんなとき、簡単・正確に直径を割り出すライフハックを紹介するよ！
　やりかたは簡単。
　手近にあるコピー用紙とか封筒とか、とにかく直角な紙を用意して、その角を印刷可能な円の範囲の端(たとえば点A)に当てるだけ！
　そしたら、紙のフチと円の端が交わるところ(点Bと点C)に印をつけて、その間の距離を定規で測れば、それが直径の長さなんだ！ふしぎ！
　これで0.1ミリ単位での印刷範囲設定ができるね！


　別にライフハックでもなんでもないし、CD-R印刷なんて滅多にしないし、0.1ミリの精度で測るには定規の目盛りが足りないし、そもそもそんな精度を必要としていない。
　ただ、中学校で習う「直径に対する円周角は直角である」という定理（ターレスの定理）が、事務職でも役に立つことがある、という事例を見つけたので記録しておくだけ。
　中学生から「実生活で何の役にたつのか」という質問を受けがちな幾何学だが、将来そのような的外れな質問をうけたときの的外れなカウンターとしてとっておこうと思う。

[LINK] [COMMENT]