◆匿名ツッコミフォーム◆
以下の記事へのツッコミです
■2019-03-01 ： こんぺいとうコンビネーション
たまにカロリー補給のために春日井製菓のこんぺいとうを買うんだけど、その袋にこんなことが書いてある。
「5種類の混合には注意しておりますが、全種類入らない場合があります。」
あるのか？ 俺は直ちに動き出した。
容量は105グラムとある。10粒まとめて計量しおよその重量を出して、1袋平均116粒と推定。こんぺいとうの種類は「プレーン」「ぶどう」「もも」「りんご」「サイダー」の5種類である。
何はともあれ、入っている粒の組み合わせのパターンを数え上げなければならない。となると5種類の粒が116個あるから……5の116乗！？ いやまさかそんな無慈悲な数がいきなり出てくるわけがない。
順番は関係ないわけだから、とにかく最終的に入っている数のパターンを知りたい。それなら多少は計算可能な数字が出てくるはずだ。ここで俺はセンター試験でアホほどやった Combination のことを思い出すことになった。
この問題は、センター試験でアホほどやった「116個のボールをA、B、C、D、Eの箱に分けるパターンは全部で何通りあるか求めよ」という、いわゆる順列組み合わせの問題ではないか。いやさすがに試験では116個とか無謀な数ではなかったけれども。
となれば復習タイムだ。
たとえば「味が3種類あるこんぺいとうが無数にあり，その中から5つ取り出したときのパターンの総数」は、「互いに区別のないボール5個を、区別のある箱3個に分配する」と置き換えることができる。この場合の計算はこんな感じだった。
これを応用して、5種類のこんぺいとうが116粒入っている場合のパターンの総数は、
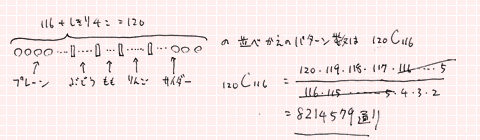8214570通りと計算できる。……①
次に、先ほどの条件に「どの箱もひとつ以上ボールが入っていること」という条件を加える。これが「全種類入っている場合」のパターンとなる。0を除くのもセンター試験でアホほどやったパターンだ。この場合はスキマに注目する。
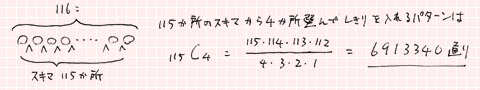6913340通りあることがわかった。……②
そして①－②により、「全種類が揃わないパターン」の総数が求められる。その数なんと1301230通り。
あとは1301230÷8214570≒0.158で答えはおよそ15.8％……ってアレ？
いい加減にしろよな……15.8％の確率で揃わないなんてことがあるはずがないじゃあないか……俺が計算をミスったと言いたいんだろ！？ そんなことはわかってるんだよッ！ だから計算機とエクセルさんとコンビネーション計算サイトで3回も検算してんだよ俺は！ その結果がこの仕打ちか！ 116粒もあるって言っときながらなんで6袋に1袋くらいの割合で不良品が出る計算になってんだこの……クサレ脳ミソがァーッ！
……冷静になれ。人を見下す言い方は良くない。どこかに落とし穴があるはずだ……。
事例をもっと単純にするんだ……区別のないコイン2枚を投げたときに出るパターンは「表・表」「表・裏」「裏・裏」の3パターン……しかし「表・表」が出る確率は1/3では……ない！
ああっ……！ そうか！ パターンを列挙したからといって、どのパターンも等確率で出るなんて保証はない！
僕は馬鹿だ……。Combination のことにかまけるばかり、こんなに大事なことを見落とすなんて……。
こうなれば統計的手段に訴えたほうが早い。俺は大量のデータを集めることにした。
ここで実際にこんぺいとうを買い占めて開封し内訳を数えていったほうが“映える”のはわかっているが、時間も予算もないのでヴァーチャルな解決法を採用する。「ランダムに0から4の箱を選び数字を+1することを116回くりかえす」だけのプログラムを書き、それをさしあたって5000周ほどぶん回した。
こうして一瞬にして5000袋の仮想こんぺいとうが開封され、内訳が明らかになった。
出力された結果をエクセルさんにコピーし、試しにプレーン味の個数を度数分布表にぶちこんでみると……。
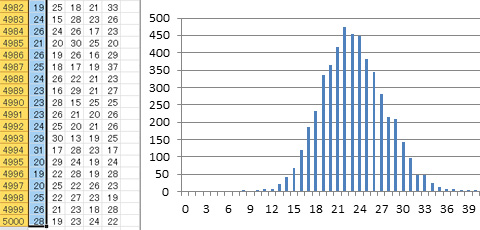こいつ……見たことがあるぞ……たしか正規分布って奴じゃあないのか？
正規分布と仮定してしまえばやるべきことは定まってくる。必要なのは平均値と標準偏差だ。それぞれ AVERAGE 関数と STDEV.S 関数で引っ張ってこれる。
あとはその２つを NORM.DIST 関数に食わせてやれば、プレーン味が23個入っている確率やら10粒入っている確率やらを個別に推計できる。1粒も入っていない確率もこれで出すことができるというわけだ。
計算してみると、平均値に近い23粒を中心に、16粒～30粒の間に収まる確率が90％を越える。今回の5000オーダーの中で最も少なかったのは8粒で、確率としては0.02％。そして待望の1粒も入らない確率は、およそ0.0000062％であった。
これが5種類それぞれに起こりうるので5倍する。2色以上欠ける確率が重複するので厳密に言うと5倍でないが、確率が確率なので無視してしまおう。となるとおよそ0.00003％。これが冒頭の疑問への答えとなる。
というわけで結論ッ！
このこんぺいとうの注意書きが機能する確率は、およそ1000万分の3！
年末ジャンボ宝くじの一等がヒットするのがおよそ1000万分の1と言われているのでとんでもない確率のように見えるが、それでも年間に100万袋くらい生産し続ければ、数年で遭遇しないともいえないくらいの確率である。少なくとも猿がワープロでシェイクスピアの一節を打ち出すよりは高いと思われる。春日井製菓の末永いご発展をお祈り申し上げます。
この記事は脳内格闘の過程を書き出したものなので、統計ガチ勢や数学ガチ勢からすれば非常に稚拙なものと思われますが、暖かい眼で見守っていただければ幸いです。
「5種類の混合には注意しておりますが、全種類入らない場合があります。」
あるのか？ 俺は直ちに動き出した。
容量は105グラムとある。10粒まとめて計量しおよその重量を出して、1袋平均116粒と推定。こんぺいとうの種類は「プレーン」「ぶどう」「もも」「りんご」「サイダー」の5種類である。
何はともあれ、入っている粒の組み合わせのパターンを数え上げなければならない。となると5種類の粒が116個あるから……5の116乗！？ いやまさかそんな無慈悲な数がいきなり出てくるわけがない。
順番は関係ないわけだから、とにかく最終的に入っている数のパターンを知りたい。それなら多少は計算可能な数字が出てくるはずだ。ここで俺はセンター試験でアホほどやった Combination のことを思い出すことになった。
この問題は、センター試験でアホほどやった「116個のボールをA、B、C、D、Eの箱に分けるパターンは全部で何通りあるか求めよ」という、いわゆる順列組み合わせの問題ではないか。いやさすがに試験では116個とか無謀な数ではなかったけれども。
となれば復習タイムだ。
たとえば「味が3種類あるこんぺいとうが無数にあり，その中から5つ取り出したときのパターンの総数」は、「互いに区別のないボール5個を、区別のある箱3個に分配する」と置き換えることができる。この場合の計算はこんな感じだった。
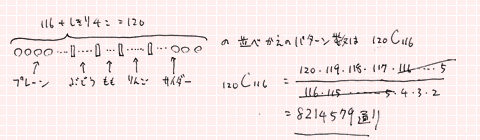
次に、先ほどの条件に「どの箱もひとつ以上ボールが入っていること」という条件を加える。これが「全種類入っている場合」のパターンとなる。0を除くのもセンター試験でアホほどやったパターンだ。この場合はスキマに注目する。
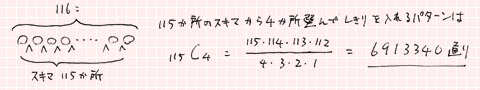
そして①－②により、「全種類が揃わないパターン」の総数が求められる。その数なんと1301230通り。
あとは1301230÷8214570≒0.158で答えはおよそ15.8％……ってアレ？
いい加減にしろよな……15.8％の確率で揃わないなんてことがあるはずがないじゃあないか……俺が計算をミスったと言いたいんだろ！？ そんなことはわかってるんだよッ！ だから計算機とエクセルさんとコンビネーション計算サイトで3回も検算してんだよ俺は！ その結果がこの仕打ちか！ 116粒もあるって言っときながらなんで6袋に1袋くらいの割合で不良品が出る計算になってんだこの……クサレ脳ミソがァーッ！
……冷静になれ。人を見下す言い方は良くない。どこかに落とし穴があるはずだ……。
事例をもっと単純にするんだ……区別のないコイン2枚を投げたときに出るパターンは「表・表」「表・裏」「裏・裏」の3パターン……しかし「表・表」が出る確率は1/3では……ない！
ああっ……！ そうか！ パターンを列挙したからといって、どのパターンも等確率で出るなんて保証はない！
僕は馬鹿だ……。Combination のことにかまけるばかり、こんなに大事なことを見落とすなんて……。
こうなれば統計的手段に訴えたほうが早い。俺は大量のデータを集めることにした。
ここで実際にこんぺいとうを買い占めて開封し内訳を数えていったほうが“映える”のはわかっているが、時間も予算もないのでヴァーチャルな解決法を採用する。「ランダムに0から4の箱を選び数字を+1することを116回くりかえす」だけのプログラムを書き、それをさしあたって5000周ほどぶん回した。
こうして一瞬にして5000袋の仮想こんぺいとうが開封され、内訳が明らかになった。
出力された結果をエクセルさんにコピーし、試しにプレーン味の個数を度数分布表にぶちこんでみると……。
正規分布と仮定してしまえばやるべきことは定まってくる。必要なのは平均値と標準偏差だ。それぞれ AVERAGE 関数と STDEV.S 関数で引っ張ってこれる。
あとはその２つを NORM.DIST 関数に食わせてやれば、プレーン味が23個入っている確率やら10粒入っている確率やらを個別に推計できる。1粒も入っていない確率もこれで出すことができるというわけだ。
計算してみると、平均値に近い23粒を中心に、16粒～30粒の間に収まる確率が90％を越える。今回の5000オーダーの中で最も少なかったのは8粒で、確率としては0.02％。そして待望の1粒も入らない確率は、およそ0.0000062％であった。
これが5種類それぞれに起こりうるので5倍する。2色以上欠ける確率が重複するので厳密に言うと5倍でないが、確率が確率なので無視してしまおう。となるとおよそ0.00003％。これが冒頭の疑問への答えとなる。
というわけで結論ッ！
このこんぺいとうの注意書きが機能する確率は、およそ1000万分の3！
年末ジャンボ宝くじの一等がヒットするのがおよそ1000万分の1と言われているのでとんでもない確率のように見えるが、それでも年間に100万袋くらい生産し続ければ、数年で遭遇しないともいえないくらいの確率である。少なくとも猿がワープロでシェイクスピアの一節を打ち出すよりは高いと思われる。春日井製菓の末永いご発展をお祈り申し上げます。
この記事は脳内格闘の過程を書き出したものなので、統計ガチ勢や数学ガチ勢からすれば非常に稚拙なものと思われますが、暖かい眼で見守っていただければ幸いです。