◆匿名ツッコミフォーム◆
以下の記事へのツッコミです
■2009-11-03 ： 文化の比
唐突に「定規とコンパスだけで正五角形を作図せよ」という問題が出された。
ちょっと考えたがサッパリわからない。
敵を知らずして闘いに臨むべきではなかろう。
まずは正五角形の特徴を調べることにした。
いきなり正五角形の作図法を調べても、理解も証明も困難だろう、という判断だ。
まず、正多角形なので、全ての辺の長さが一緒だ。
内角は108度。煩悩の角度である。３つの三角形に分断して証明した覚えがある。
特筆すべきは、辺の長さと、対角線の長さの比率が「黄金比」になっている点だ。
ややめんどくさいが、三角形の合同＆相似と解の公式を使えば証明できる。
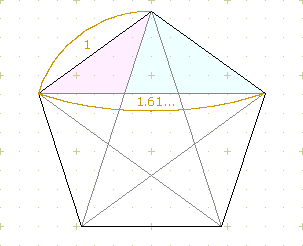黄金比。聞いたことがあるか？
およそ1:1.618。これは古代から最も美しい形の基本の比率とされている。
『パルテノン神殿』『ミロのビーナス』……この世の建築・美術の傑作群には、偶然なのか？あるいは計算なのか？この黄金比が隠されている。
自然界にもたびたび現れる比率だ、とロバート・ラングドン先生も言っていた。
ちなみに正方形の一辺と対角線の比(1:1.41…)は「白銀比」と呼ばれ、コピー用紙とかに使われている。
なるほど、正四角形が白銀比で、正五角形が黄金比ってわけか。
とにかくその黄金比が得られれば、五角形の辺の長さから対角線の長さが分かるわけで、コンパスで残りの点をガチャガチャ探り当てて、この問題はゲームセットだ。
黄金比、黄金比……
まて……芸術家たちはどこから「黄金比」を学んだ？
「美しさの基本」とかを、どこで？
学者から聞いたり、定規で計ったわけじゃあないはずだ……
それはコピーってやつで、本物じゃあない……本物があるはずだ！
ぼくが……今！この目で見ているものでいいのか！？
今までにも！すでに！さっきからも！見ているもので！！
LESSON4……敬意を払え！
（イラストはイメージです） 俺の肉体で五角形を作図するッ！
どこかがきっと黄金比なハズだァー！！
真面目な解答は、真面目な黄金比の作図法を調べていただければ、中学校の数学ツールだけでも辿り着けると思うので、割愛。
ちょっと考えたがサッパリわからない。
敵を知らずして闘いに臨むべきではなかろう。
まずは正五角形の特徴を調べることにした。
いきなり正五角形の作図法を調べても、理解も証明も困難だろう、という判断だ。
まず、正多角形なので、全ての辺の長さが一緒だ。
内角は108度。煩悩の角度である。３つの三角形に分断して証明した覚えがある。
特筆すべきは、辺の長さと、対角線の長さの比率が「黄金比」になっている点だ。
ややめんどくさいが、三角形の合同＆相似と解の公式を使えば証明できる。
およそ1:1.618。これは古代から最も美しい形の基本の比率とされている。
『パルテノン神殿』『ミロのビーナス』……この世の建築・美術の傑作群には、偶然なのか？あるいは計算なのか？この黄金比が隠されている。
自然界にもたびたび現れる比率だ、とロバート・ラングドン先生も言っていた。
ちなみに正方形の一辺と対角線の比(1:1.41…)は「白銀比」と呼ばれ、コピー用紙とかに使われている。
なるほど、正四角形が白銀比で、正五角形が黄金比ってわけか。
とにかくその黄金比が得られれば、五角形の辺の長さから対角線の長さが分かるわけで、コンパスで残りの点をガチャガチャ探り当てて、この問題はゲームセットだ。
黄金比、黄金比……
まて……芸術家たちはどこから「黄金比」を学んだ？
「美しさの基本」とかを、どこで？
学者から聞いたり、定規で計ったわけじゃあないはずだ……
それはコピーってやつで、本物じゃあない……本物があるはずだ！
ぼくが……今！この目で見ているものでいいのか！？
今までにも！すでに！さっきからも！見ているもので！！
LESSON4……敬意を払え！
（イラストはイメージです）
どこかがきっと黄金比なハズだァー！！
真面目な解答は、真面目な黄金比の作図法を調べていただければ、中学校の数学ツールだけでも辿り着けると思うので、割愛。