正方形を分割して組み替えたら、あら不思議！面積が増えた！的なパズルがある。
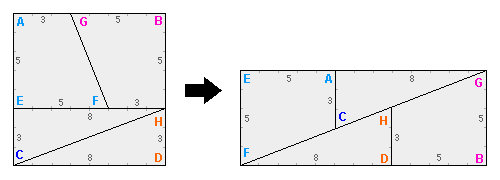
　図をご覧いただきたい。8×8＝64平方cmの正方形を分割して組み替えたら、5×13＝65平方cmになっている。面積が増えた！やった！金塊でこれをやったら大金持ちだ！

　…と言いたいところだけど、お察しの通り、１平方cmぶん隙間ができているだけだ。



　実際に厳密に組み替えて「ここが歪んでるから面積が増えたように見えるんだよ」と指摘するのは簡単である。しかし、「うるさいそれはオマエのハサミが曲がってるんだ、数学的に証明してみろ」と言われたらどのように説明するだろうか。
　「ハサミを振り上げる」とか「カラテする」とかは無しの方向で考えてみたい。

　まっさきに思いつくのは各図形の面積を求めて足すことだが、それは元の正方形の面積を計算しなおしただけであり、それを組み替えて面積が増えたように見える理由を示すことはできない。
　とりあえず真面目に中学３年レベルの数学で証明する方法と、中学１年レベルの数学でなんとかする方法を思いついた。
　数学好きはヒマなときにでも考えてみるとおもしろいと思うよ。

理数 [COMMENT]